In 1984, Adi Shamir[1] proposed a new cryptographic primitive, identity-based cryptosystem(IBC). However, Shamir only gave a construction of identity-based signature(IBS) rather than IBE which remained open for many years. In 2001, Boneh-Franklin[2] and Cock seperately proposed their schemes of IBE. This post only talks about the BF-IBE scheme. In a previous post, we talked about pairing, which is a basis of BF-IBE and you should read it at first.

1 motivation

As everyone knows, PKC(public key cryptography) solved the problem of symmetric key distribution, and PKI(public key infrastructure) solved the problem of public key distribution by introducing TTP(trusted-third party), CA for instance. Then TTP of PKI has to store large volume of certificates and the clients should acquire server's certification before authentication.

While within IBE, the receiver's ID is just his public key, such that no additional resource or extra round of communication is needed for the certificates.

Since IDs can be random strings, IBE allows a random string as public key, which is dissatisfied in tranditional PKC (RSA, Elgamal, ECC, etc.).

2 Boneh-Franklin IBE

In this part, we are going to describe the Boneh-Franklin IBE scheme. BF-IBE involves three roles as the following figure describes.

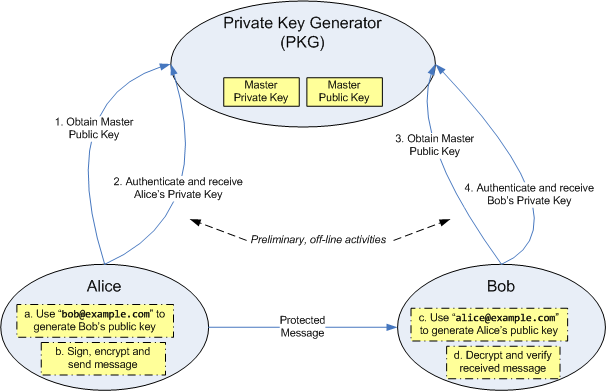
Alice, the sender would like to transmit some message to the receiver, Bob, under the protection of BF-IBE. A thirdparty named PKG(Private Key Generator) is introduced, and it is critical to the whole scheme.

The algorithms:

1. \(Setup(\tau)\).

Step 1. Generate an admissible bilinear map \(\hat{e}:\mathbb{G}_1\times \mathbb{G}_1\rightarrow \mathbb{G}_2\), \(\mathbb{G}_1, \mathbb{G}_2\) are of prime order \(q\), and choose a random generator \(P\in \mathbb{G}_1\).

Step 2. Pick a random \(s\in \mathbb{Z}_q\), and set \(P_{pub}=sP\).

Step 3. Choose cryptographic hash functions \(H_1:\{0,1\}^\ast \rightarrow \mathbb{G}_1^\ast\), \(H_2:\mathbb{G}_2\rightarrow \{0,1\}^n\).

The plaintext space is \(\mathcal{M}=\{0,1\}^n\), ciphertext space is \(\mathcal{C}=\mathbb{G}_1^\ast\times\{0,1\}^n\). The public parameter is \(Param=<q,\mathbb{G_1},\mathbb{G_2},\hat{e},n,P,P_{pub},H_1,H_2>\). And the master key(\(MK\)) is \(s\in \mathbb{Z}_q^\ast\)

2. \(Extract(ID)\). Private key of \(ID\) is \(d_{ID}=sQ_{ID}=sH_1(ID)\)

3. \(Encrypt(M)\). \(C=<rP, M\oplus H_2(g_{ID}^r)>\), where \(g_{ID}=\hat{e}(Q_{ID}, P_{pub})\)

4. \(Decrypt(C=<U,V>)\). \(M=V\oplus H_2(\hat{e}(d_{ID},U))\).

3 correctness

\[V\oplus H_2(\hat{e}(d_{ID},U))=M\oplus H_2(g_{ID}^r)\oplus H_2(\hat{e}(d_{ID},U))\]

\[H_2(g_{ID}^r)\oplus H_2(\hat{e}(d_{ID},U))=H_2(\hat{e}(Q_{ID},sP)^r)\oplus H_2(\hat{e}(sQ_{ID},rP))=0^n\]

References